ACCV 2016 Tutorial, November 2016, Taipei, Taiwan
Title
Fitting Ellipse and Computing Fundamental Matrix and Homography
Date, Time, and Venue
Thursday 24 November, 2016
9:00am - 12:20pm (with a tea break in between)
Room 201D
Abstract
Computational techniques for ellipse fitting, fundamental matrix
computation, and homogrphy computation have extensively been studied
since the 1980s, but significant progress was made only in the 2010s.
This lecture introduces the latest state of the art.
Lecturer

Kenichi Kanatani
(biography),
Professor Emeritus,
Okayama University, Japan.
Contents
- Introduction
- Ellipse Fitting
- Algebraic fitting
- Non-iterative: least squares, Taubin method, HyperLS
- Iterative: iterative reweight, renormalization, hyper-renormalization
- Geometric fitting
- Sampson error minimization, FNS
- Geometric distance minimization
- Hyperaccurate correction
- Robust fitting
- Outlier removal: RANSAC
- Ellipse-specific fitting: Fitzgibbon et al., penalty method, random sampling
- Fundamental Matrix Computation
- Imposition of rank constraint
- A posteriori correction: SVD correction, optimal correction
- Hidden variable approach
- Extended FNS
- Geometric distance minimization
- Homography Computation
- Algebraic method
- Non-iterative: least squares, Taubin method, HyperLS
- Iterative: iterative reweight, renormalization, hyper-renormalization
- Geometric method
- Sampson error minimization, FNS
- Geometric distance minimization
- Hyperaccurate correction
- Summary
Materials
This lecture is based on the following two books:
-
K. Kanatani, Y. Sugaya, and Y. Kanazawa,
Ellipse Fitting for Computer Vision: Implementation and Applications
(online version)
Morgan & Claypool Publishers, San Rafael, CA, U.S., April, 2016.

-
K. Kanatani, Y. Sugaya, and Y. Kanazawa,
Guide to 3D Vision Computation: Geometric Analysis and Implementation,
Springer International, Cham, Switzerland, December, 2016.

The slide
of
this lecture is available on line here.
Ellipse demo excerpts
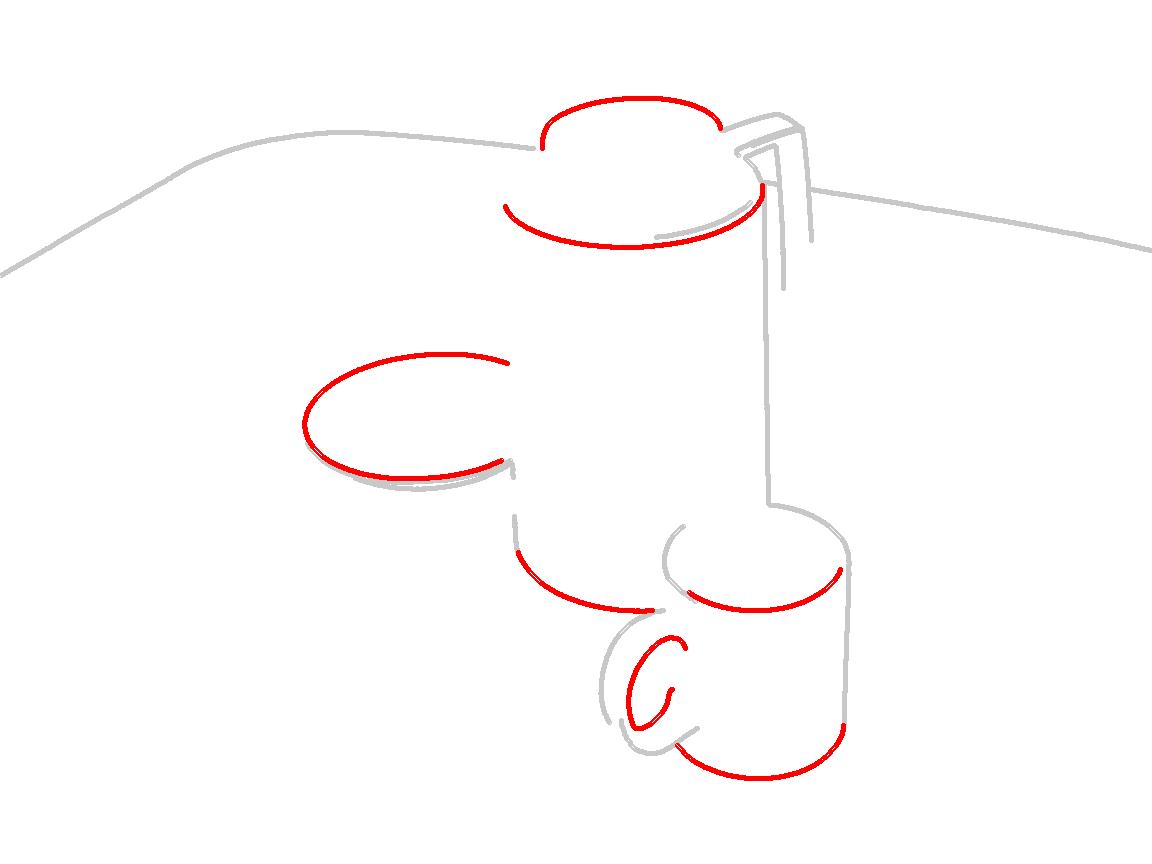





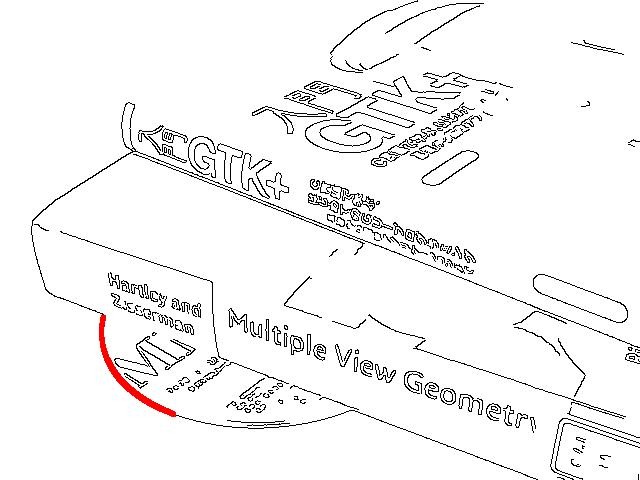
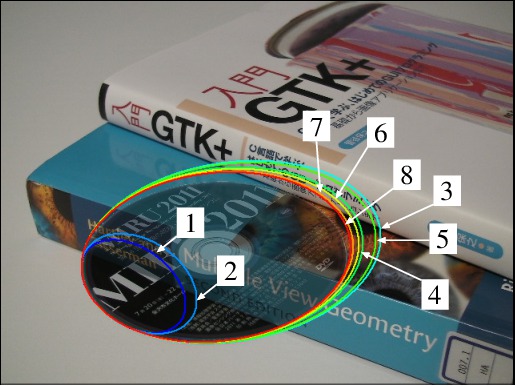
1. LS,
2. iterative reweight,
3. Taubin,
4. renormalization,
5. HyperLS,
6. hyper-renormalization,
7. FNS,
8. FNS + hyperaccurate correction
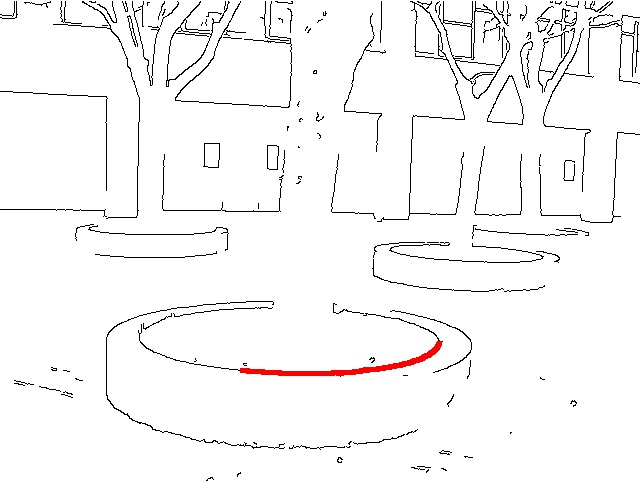


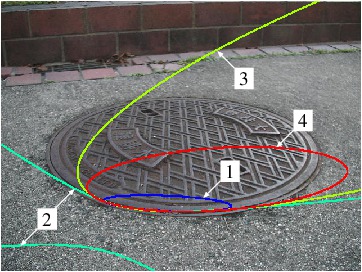
1. Fitzgibbon et al., 2. hyper-renormalization, 3. penalty method,
4. random sampling














